Дискретные модели электрической цепи
С применением любого неявного метода интегрирования дифференциальных уравнений можно составить эквивалентную схему электрической цепи, содержащую только действующие в цепи источники, резистивные элементы и зависимые источники, заменяющие индуктивные и емкостные элементы. Режим такой схемы описывается не системой дифференциальных уравнений, а системой алгебраических уравнений, которые составляются и решаются теми же методами, что и для цепей постоянного и переменного токов (с уравнениями Кирхгофа, контурными токами, узловыми потенциалами).
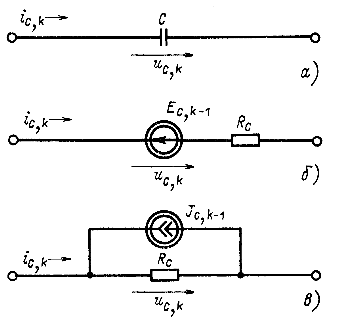
Рассмотрим замену индуктивного и емкостного элементов. Для индуктивного элемента (рис. 14.43, a) ![]() , откуда следует, что в момент
, откуда следует, что в момент ![]() ток
ток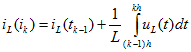
или с применением среднего значения интеграла (метод трапеций)![]()
Обозначив
![]()
получим
![]()
Этому соотношению между током и напряжением индуктивного элемента для k-го шага соответствует эквивалентная схема или дискретная модель на рис. 14.43, б. При постоянном шаге h сопротивление ![]() не изменяется от шага к шагу; ток источника зависит от значений тока и напряжения элемента на предыдущем шаге. Источник тока можно по известному правилу заменить источником ЭДС
не изменяется от шага к шагу; ток источника зависит от значений тока и напряжения элемента на предыдущем шаге. Источник тока можно по известному правилу заменить источником ЭДС ![]() (рис. 14.43, в).
(рис. 14.43, в).
Для емкостного элемента (рис. 14.44, а) ![]() , откуда следует, что в момент
, откуда следует, что в момент ![]() напряжение
напряжение
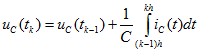
или с применением среднего значения интеграла
![]()
Обозначив
![]()
получим
![]()
Эквивалентная схема или дискретная модель показана на рис. 14.44, б. Источник ЭДС можно заменить источником тока ![]() (рис. 14.44, в).
(рис. 14.44, в).
В системе уравнений, составленной после замены индуктивных и емкостных элементов, например методом контурных токов ![]() или методом узловых потенциалов
или методом узловых потенциалов ![]() , матрицы
, матрицы ![]() при постоянном шаге достаточно вычислить 1 раз, что упрощает составление программ.
при постоянном шаге достаточно вычислить 1 раз, что упрощает составление программ.
Отметим, что формирование уравнений с переменными состояния (см. раздел) более трудоемко по сравнению с получением уравнений для дискретной модели.
Чтобы составить дискретные модели для момента времени ![]() , необходимо знать начальные значения всех величин, входящих в составляемую систему уравнений.
, необходимо знать начальные значения всех величин, входящих в составляемую систему уравнений.
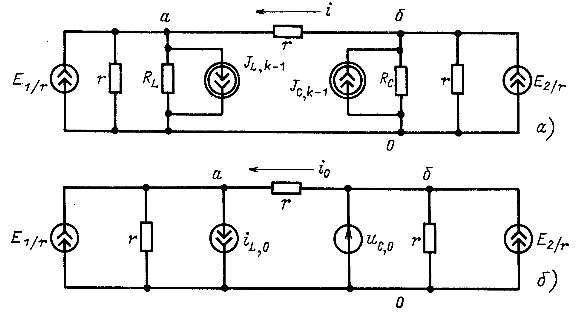
На рис. 14.45, а представлена дискретная модель с зависимыми и независимыми источниками тока для цепи на рис. 14.28. Модель имеет три узла. Расчет целесообразно выполнить методом узловых потенциалов.
Матрица проводимостей
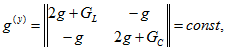
Рис. 14.43
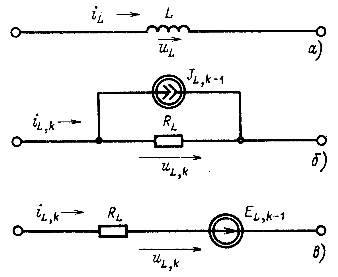
Рис. 14.44
где ![]() . Независимые начальные условия (см. рис. 14.28)
. Независимые начальные условия (см. рис. 14.28) ![]() . Для вычисления начальных значений потенциалов необходимо заменить индуктивный и емкостный элементы источниками
. Для вычисления начальных значений потенциалов необходимо заменить индуктивный и емкостный элементы источниками ![]() (рис. 14.45, б). Как следует из рис. 14.45, б, потенциалы
(рис. 14.45, б). Как следует из рис. 14.45, б, потенциалы ![]() , где
, где ![]() .
.
Рис. 14.45
Для расчета режима дискретной модели можно, когда это целесообразно, выбрать и метод расширенных узловых уравнений (см. раздел), в том числе и для цепей с управляемыми источниками.
Дискретные модели (см. рис. 14.43, б, в и 14.44, б, в) составлены с применением метода трапеций. Как указывалось, дискретные модели можно получить и на основе иных неявных алгоритмов, но, конечно, другие.
Пример 14.8.
Для цепи примера 14.6 составить дискретную модель с источниками ЭДС. Записать уравнения для расчета токов ![]() методом контурных токов.
методом контурных токов.
Решение. Дискретная модель цепи показана на рис. 14.46. Выбрав в качестве контурных токи ![]() , запишем уравнения
, запишем уравнения
![]()
где согласно (14.107)
![]()
Рис. 14.46
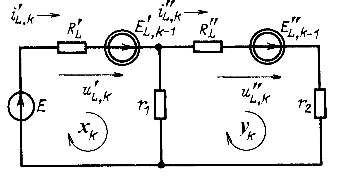
Из той же схемы на рис. 14.46 находим для предыдущего шага ![]() (левый контур);
(левый контур); ![]() (правый контур).
(правый контур).
После подстановки этих выражений и численных значений в уравнения контурных токов получаем систему уравнений
![]()
Решение совпадает с результатами, приведенными в примере 14.7 при расчете методом трапеций (табл. 14.4), так как дискретные модели на рис. 14.43 и 14.44 были составлены также с применением метода трапеций.
Переходные процессы
Переходные процессы в электрических цепях
Законы коммутации
Переходный, установившийся и свободный процессы
Короткое замыкание rL-цепи
Включение rL-цепи на постоянное напряжение
Включение rL-цепи на синусоидальное напряжение
Короткое замыкание rС-цепи
Включение rC-цепи на постоянное напряжение
Включение rC-цепи на синусоидальное напряжение
Переходные процессы в rС-цепи
Апериодическая разрядка конденсатора
Предельный случай апериодической разрядки конденсатора
Периодическая (колебательная) разрядка конденсатора
Включение rLC-цепи на постоянное напряжение
Общий случай расчета переходных процессов классическим методом
Пример классического метода
Переходные процессы в цепях с взаимной индуктивностью
Включение пассивного двухполюсника к источнику непрерывно меняющегося напряжения
Включение пассивного двухполюсника к источнику напряжения произвольной формы
Переходная и импульсная переходная характеристики
Запись интеграла Дюамеля при помощи импульсной переходной характеристики
Метод переменных состояния
Численные методы решения уравнений состояния
Дискретные модели электрической цепи
Переходные процессы при некорректных коммутациях
Определение переходного процесса при воздействии периодических импульсов напряжения