Электромагнитные колебания и волны (страница 2)
Излучение электромагнитных волн
1. К антенне длиной l=2 м подводится синусоидальный ток с амплитудой ![]() и частотой
и частотой ![]() . Показать, что такую систему можно рассматривать как электрический диполь, и вычислить напряженность электрического поля в воздухе на расстоянии r=50 км (в волновой зоне) под углом
. Показать, что такую систему можно рассматривать как электрический диполь, и вычислить напряженность электрического поля в воздухе на расстоянии r=50 км (в волновой зоне) под углом ![]() к оси диполя.
к оси диполя.
Решение. Длина волны ![]() . Так как
. Так как ![]() , то можно приближенно считать, что I=const по длине антенны, т. е. что антенну можно рассматривать как электрический диполь. В волновой (дальней) зоне меридиальная компонента поля
, то можно приближенно считать, что I=const по длине антенны, т. е. что антенну можно рассматривать как электрический диполь. В волновой (дальней) зоне меридиальная компонента поля
![]()
так как r=50 км и ![]() , то зона будет дальней (волновой).
, то зона будет дальней (волновой).
2. Электрическая антенна в виде провода длиной l=3 м питается синусоидальным током с частотой ![]() и амплитудой
и амплитудой ![]() . Вычислить мощность и сопротивление излучения антенны.
. Вычислить мощность и сопротивление излучения антенны.
Решение. Так как длина волны ![]() , то антенну можно рассматривать как электрический диполь.
, то антенну можно рассматривать как электрический диполь.
Мощность излучения антенны:![]()
Сопротивление излучения
![]()
Распространение электромагнитных волн
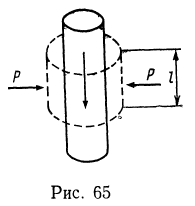
3. По прямолинейному проводнику радиуса а течет постоянный ток с плотностью j. Показать, что энергия, втекающая в проводник и обусловленная существованием вектора Умова—Пойтинга, на отрезке провода длиной l равна джоулевым потерям энергии в рассматриваемом объеме проводника. Проводимость проводника равна ![]() .
.
 Решение. Электрическое поле
Решение. Электрическое поле
![]()
магнитное поле
![]()
Так как электрическое поле направлено вдоль провода (рис. 65), а магнитное перпендикулярно к проводу, то вектор Умова—Пойтинга направлен внутрь провода и равен
![]()
Следовательно, поток вектора Умова—Пойтинга через поверхность, охватывающую провод, равен
![]()
С другой стороны, потери на джоулево тепло определяются интегралом:
![]()
Сравнивая (4) и (5), приходим к выводу, что потери на джоулево тепло в проводнике компенсируются энергией, втекающей в виде волн в проводник из свободного пространства.
4. Воздушная двухпроводная линия из медных проводов характеризуется следующими параметрами: активное сопротивление ![]() , индуктивность
, индуктивность ![]() , емкость
, емкость ![]() , проводимость изоляции между проводами (утечка)
, проводимость изоляции между проводами (утечка) ![]() . Линия предназначена для работы на частоте 20 кГц. Определите волновое сопротивление линии
. Линия предназначена для работы на частоте 20 кГц. Определите волновое сопротивление линии ![]() коэффициент распространения
коэффициент распространения ![]() , коэффициент затухания
, коэффициент затухания ![]() и коэффициент фазы
и коэффициент фазы ![]() . Рассчитать длину бегущей волны
. Рассчитать длину бегущей волны ![]() и ее фазовую скорость
и ее фазовую скорость ![]() . Решите задачу в приближении
. Решите задачу в приближении ![]() . Проверьте справедливость этого приближения для рассматриваемой линии.
. Проверьте справедливость этого приближения для рассматриваемой линии.
Решение. По определению
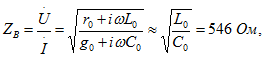
так как ![]() , и
, и
![]()
В том же приближении ![]() имеем
имеем
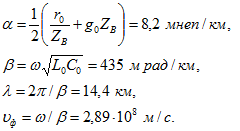
Проверим справедливость использованного приближения:
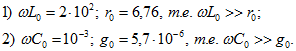
5. Определить коэффициент затухания двухпроводной линии, если мощность генератора составляет 0,1 Вт и на приемнике (на согласованной с линией нагрузке) должна выделяться мощность 100 мкВт. Длина линии равна 10 км.
Решение. По определению затухание равно
![]()
Коэффициент затухания линии должен быть равен
![]()
6. Двухпроводная линия из медных проводов предназначена для телефонной связи на частоте ![]() . Первичные параметры линии равны:
. Первичные параметры линии равны: ![]() . Вычислить индуктивность
. Вычислить индуктивность ![]() , которую надо включить на каждый километр длины, чтобы линия стала неискажающей.
, которую надо включить на каждый километр длины, чтобы линия стала неискажающей.
Решение. Линия не будет вносить искажений, если затухание и скорость распространения волн не будут зависеть от частоты. Для этого должно выполняться условие
![]()
где ![]() — добавочная индуктивность на единицу длины линии. Из (1) находим
— добавочная индуктивность на единицу длины линии. Из (1) находим
![]()
7. Линия без потерь, параметры которой ![]() , нагружена на чисто активное сопротивление
, нагружена на чисто активное сопротивление ![]() , где
, где ![]() — волновое сопротивление линии. Определить коэффициенты отражения
— волновое сопротивление линии. Определить коэффициенты отражения ![]() , бегущей волны
, бегущей волны ![]() , стоячей волны
, стоячей волны ![]() .
.
Решение. Волновое сопротивление линии
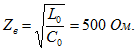
Сопротивление нагрузки
![]()
Коэффициент отражения
![]()
Коэффициент бегущей волны
![]()
Коэффициент стоячей волны
![]()
8. Получите выражения для фазовой и групповой скоростей простейшей волны, распространяющейся в прямоугольном волноводе шириной а и высотой b метров.
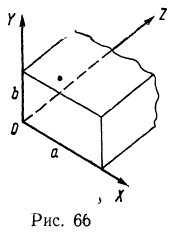 Решение. Пусть оси координат направлены так, как указано на рис. 66. В простейшем случае имеется только одна компонента вектора напряженности электрического поля
Решение. Пусть оси координат направлены так, как указано на рис. 66. В простейшем случае имеется только одна компонента вектора напряженности электрического поля ![]() , т. е.
, т. е. ![]() должна иметь вид плоской волны
должна иметь вид плоской волны
![]()
и удовлетворять волновому уравнению
![]()
Подставим (1) в волновое уравнение (2), получим
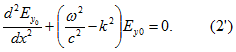
Как известно, простейшее решение уравнения (2‘) имеет вид
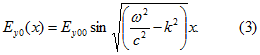
Так как поле Е перпендикулярно поверхности волновода, то при х=а
![]()
Предполагая, что ![]() , получим в простейшем случае
, получим в простейшем случае
![]()
или![]()
По определению, фазовая скорость равна
![]()
Используя (5′), получим
![]()
Аналогично, групповая скорость
![]()
Сравнивая (6′) и (7), легко заметить, что
![]()
9. Найдите минимальную частоту для простейшего типа волны, распространяющейся в прямоугольном волноводе шириной а и высотой b метров.
Решение. Граничные условия в волноводе (см. задачу 8.) приводят к выражению
![]()
Так как ![]() , то минимальная частота равна
, то минимальная частота равна
![]()
10. Выразите длину волны в волноводе ![]() через длину волны в свободном пространстве
через длину волны в свободном пространстве ![]() в случае простейшего типа волн, распространяющихся в прямоугольном волноводе шириной а и высотой b метров.
в случае простейшего типа волн, распространяющихся в прямоугольном волноводе шириной а и высотой b метров.
Решение. Фазовая скорость волны (см. задачу 8.), распространяющейся в волноводе, равна
![]()
Длина бегущей волны в свободном пространстве
![]()
а в волноводе
![]()
Кроме того, длина волны в волноводе также равна
![]()
Используя (1) —(4), окончательно находим
![]()