Электрические машины постоянного тока (страница 3)
8. Электрическая машина задачи 3 была использована в качестве электродвигателя, причем при вращающем моменте ![]() ток в проводах, соединяющих электродвигатель с сетью, составил I=92,4 A; при этом напряжение, приложенное к электродвигателю, было равно 110 В.
ток в проводах, соединяющих электродвигатель с сетью, составил I=92,4 A; при этом напряжение, приложенное к электродвигателю, было равно 110 В.
Определить величину магнитного потока электродвигателя.
Решение:
Вращающий момент ![]() электродвигателя при измерении в ньютон-метрах выражается следующим образом:
электродвигателя при измерении в ньютон-метрах выражается следующим образом:
![]()
Ток ![]() в обмотке якоря электродвигателя параллельного возбуждения меньше тока I в проводах, соединяющих электродвигатель с сетью, на величину тока в цепи возбуждения:
в обмотке якоря электродвигателя параллельного возбуждения меньше тока I в проводах, соединяющих электродвигатель с сетью, на величину тока в цепи возбуждения:
![]()
Ток в цепи возбуждения определяется по закону Ома:
![]()
Следовательно, ток в цепи якоря
![]()
Встречная э. д. с, индуктируемая в обмотке якоря,
![]()
Коэффициент, объединяющий постоянные величины в выражении для вращающего момента ![]() и характеризующий конструктивные и электрические параметры машины.
и характеризующий конструктивные и электрические параметры машины.
![]()
Составим отношение постоянных коэффициентов ![]() взяв выражение и числовое значение
взяв выражение и числовое значение ![]() из задачи 3:
из задачи 3:
![]()
Отношение коэффициентов
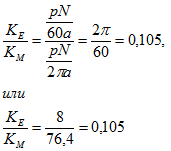
есть постоянная величина, которую полезно запомнить.
Зная вращающий момент ![]() и ток в цепи якоря
и ток в цепи якоря ![]() , можно определить коэффициент вращающего момента
, можно определить коэффициент вращающего момента ![]() , умножение которого на ток в цепи якоря дает вращающий момент:
, умножение которого на ток в цепи якоря дает вращающий момент:
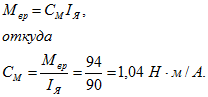
Магнитный поток
![]()
9. Электродвигатель постоянного тока отключен от сети и якорь его неподвижен. К обмотке якоря приложили постоянное напряжение 2 В, в результате чего установился постоянный ток 4 А. Затем электродвигатель пустили в ход и при напряжении 220 В, приложенном к зажимам обмотки вращающего якоря, ток в этой обмотке достиг 20 А.
Определить:
1) сопротивление цепи якоря;
2) встречную э. д. с. электродвигателя;
3) модность на входе в электродвигатель и механическую мощность;
4) ток в обмотке якоря:
а) если уменьшить скорость вращения якоря на 20% прн том же напряжении 220 В и прежних условиях в цепи возбуждения;
б) если, не отключая электродвигатель, затормозить вращение вала;
в) если произвести пуск электродвигателя, не вводя пускового реостата.
Решение:
Обмотка неподвижного якоря представляет собой пассивный элемент цепи, и сопротивление ее можно определить по закону Ома:
![]()
В обмотке вращающегося якоря индуктируется э. д. с, называемая встречной, так как она направлена встречно току. Поэтому на основании второго закона Кирхгофа
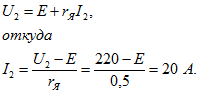
Встречная э. д. с.
![]()
Умножим величину ![]() на
на ![]() и введем в уравнение баланса мощностей
и введем в уравнение баланса мощностей
![]()
где тепловая мощность ![]() , а мощность на входе в электродвигатель
, а мощность на входе в электродвигатель
![]()
Механическая мощность
![]()
Если скорость вращения якоря уменьшится на 20% при том же напряжении ![]() и прежних условиях в цепи возбуждения, то встречная э. д. с. изменится и составит 80% от прежнего значения:
и прежних условиях в цепи возбуждения, то встречная э. д. с. изменится и составит 80% от прежнего значения:
![]()
Ток в цепи якоря возрастет и станет равным
![]()
Если вал электродвигателя затормозить, не отключая его, то получится ток
![]()
так как встречная э. д. с. в неподвижном якоре отсутствует.
Такой же величины ток возник бы при пуске электродвигателя, если не ввести реостат для ограничения тока.
10. По условиям испытания, электродвигатель постоянного тока работает при постоянном приложенном напряжении U = 220 В и при постоянном магнитном потоке. Изменение тормозного усилия от 0 до 120 Н на окружности шкива, имеющего диаметр 0,3 м, вызывает изменение по линейному закону тока от 2 до 12 А и скорости вращения якоря от 1100 до 1000 об/мин.
Определить в указанном интервале:
1) вращающий момент ![]() на ободе шкива электродвигателя;
на ободе шкива электродвигателя;
2) мощность ![]() на входе в электродвигатель и мощность
на входе в электродвигатель и мощность ![]() на его шкиве;
на его шкиве;
3) к. п. д. электродвигателя.
По числовым данным расчетов построить в одних и тех же осях координат кривые:![]()
Решение:
В случае изменения тока по линейному вакону по такому же закону изменяется и мощность на входе в электродвигатель, так как приложенное напряжение постоянно:
![]()
Вращающий момент ![]() на ободе шкива электродвигателя при динамическом равновесии равен тормозному моменту:
на ободе шкива электродвигателя при динамическом равновесии равен тормозному моменту:
![]()
Наименьшее и наибольшее значения вращающего момента пропорциональны соответствующим значениям тормозного усилия:
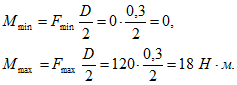
Мощность ![]() на шкиве электродвигателя связана с вращающим моментом
на шкиве электродвигателя связана с вращающим моментом ![]() следующей зависимостью:
следующей зависимостью:
![]()
Угловая скорость вращения имеет максимум
![]()
и минимум
![]()
Следовательно,
![]()
Коэффициент полезного действия ![]() , пдя случая
, пдя случая ![]()
![]()
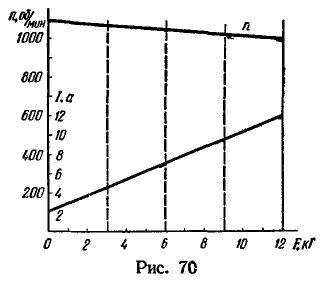
Определим промежуточные значения, построив графики ![]() (рис. 70).
(рис. 70).
Пользуясь этими графиками, можно записать в табл. 9 ряд значений F, I и n (рис. 70), соответствующих друг другу.
Таблица 9
| 0 | 27 | 49 | 83,4 | 117 |
| 2 | 4,25 | 6 | 9 | 12 |
| 1100 | 1075 | 1050 | 1025 | 1000 |
| |||||
Построим графики (рис. 71) по данным табл. 10.
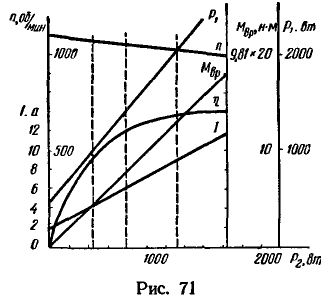
Таблица 10
| 440 | 935 | 1320 | 1980 | 2640 |
| 0 | 4,02 | 7,38 | 12,46 | 17,68 |
| 115 | 112,5 | 109,9 | 107,3 | 104,7 |
| 0 | 452,5 | 808,5 | 1337 | 1850 |
| 0 | 0,48 | 0,6 | 0,67 | 0,7 |
| |||||
11. Электродвигатель постоянного тока параллельного возбуждения имеет сопротивление цепи якоря 0,5 ом. При напряжении сети 220 В якорь электродвигателя вращается с такой скоростью и магнитный поток имеет такую величину, что противо-э. д. с. равна 210 В. Регулируя реостатом ток в цепи возбуждения, магнитный поток уменьшают до 0,9 от первоначального значения.
Какое значение примет ток по окончании переходного процесса, вызванного изменением магнитного потока, если статический момент сопротивления по валу электродвигателя, обусловленный приводимым в действие станком, остался без изменения?
Решение:
Ток в обмотке якоря до регулирования
![]()
Если уменьшить магнитный поток до ![]() , то в первое мгновение скорость вращения якоря электродвигателя не успеет измениться, противо-э. д. с. уменьшится вследствие уменьшения магнитного потока и станет равной
, то в первое мгновение скорость вращения якоря электродвигателя не успеет измениться, противо-э. д. с. уменьшится вследствие уменьшения магнитного потока и станет равной
![]()
При этом ток в обмотке якоря возрастет и достигнет значения
![]()
Новое значение тока в якоре примерно в 3 раза больше первоначального:
![]()
причем магнитный поток уменьшился всего на 10%.
Пропорциональный току в якоре ![]() и магнитному потоку Ф вращающий момент
и магнитному потоку Ф вращающий момент ![]() возрастет. Так как статический момент сопротивления на валу электродвигателя остался неизменным, то положительный момент ускорения станет увеличивать скорость вращения якоря. Однако пропорционально скорости вращения будет увеличиваться противо-э. д. с.
возрастет. Так как статический момент сопротивления на валу электродвигателя остался неизменным, то положительный момент ускорения станет увеличивать скорость вращения якоря. Однако пропорционально скорости вращения будет увеличиваться противо-э. д. с. ![]() и ток в обмотке якоря
и ток в обмотке якоря ![]() начнет уменьшаться. Ток
начнет уменьшаться. Ток ![]() будет уменьшаться до тех пор, пока вращающий момент
будет уменьшаться до тех пор, пока вращающий момент ![]() не станет равным моменту статического сопротивления
не станет равным моменту статического сопротивления ![]() на валу электродвигателя при новом значении магнитного потока, равном 0,9Ф. Поэтому ток в якоре
на валу электродвигателя при новом значении магнитного потока, равном 0,9Ф. Поэтому ток в якоре
![]()
Следовательно, значение тока в якоре увеличилось в 1,11 раза.
Скорость вращения якоря электродвигателя приняла новое (большее) установившееся значение. Если до регулирования
![]()
то после регулирования
![]()
Если пренебречь величинами ![]() , то отношение скоростей
, то отношение скоростей
![]()
Таким образом, электродвигатель продолжает работать при новой скорости вращения, в 1,11 раза превышающей прежнюю.
Несмотря на некоторые приближения при рассмотрении вопроса регулирования скорости вращения электродвигателя с помощью реостата в цепи возбуждения, данный пример в целом правильно раскрывает механизм переходного процесса, возникающего при этом регулировании.
12. Электродвигатель постоянного тока параллельного возбуждения при напряжении 220 В имеет номинальный ток 51 А, номинальную скорость вращения 1000 об/мин и ток холостого хода 3 А. Суммарное сопротивление обмотки якоря и дополнительных полюсов 0,25 Ом, сопротивление цепи возбуждения 220 Ом.
Определить:
1) к. п. д. электродвигателя при токах, составляющих 0,25; 0,50; 0,75; 1,00 и 1,25 от номинального тока;
2) скорость вращения электродвигателя при тех же токах;
3) вращающий момент на валу электродвигателя в условиях п. 1 и 2.
Примечание. Ток возбуждения не регулировали.
Построить характеристики ![]()
Решение:
Коэффициент полезного действия электродвигателя постоянного тока
![]()
где ![]() — мощность на входе в электродвигатель;
— мощность на входе в электродвигатель;![]() — мощность всех потерь энергии.
— мощность всех потерь энергии.
При холостом ходе электродвигателя:
а) потери мощности в цепи возбуждения
![]()
б) потери мощности в цепи якоря
![]()
где ![]()
в) механические потери мощности и потери в стали равны остальной части мощности холостого хода:
![]()
Из перечисленных величин при изменении тока нагрузки будут изменяться только потери мощности в цепи якоря, так как, по условию, ток в цепи возбуждения постоянен, а остальные потери мощности изменяются незначительно и считаются постоянными.
Составим табл. 11 для определения к. п. д.
Таблица 11
| 3 | 13,5 | 26 | 38,5 | 51 | 63,5 |
| 1 | |||||
| 2 | 12,5 | 25 | 37,5 | 50 | 62,5 |
| 1 | 39 | 156 | 351 | 625 | 976 |
| 660 | |||||
| 660 | 699 | 816 | 1011 | 1285 | 1636 |
| 660 | 2970 | 5720 | 8470 | 11220 | 13970 |
| 0 | 2271 | 4904 | 7459 | 9935 | 12334 |
| 0 | 0,76 | 0,85 | 0,86 | 0,88 | 0,88 |
| ||||||
Противо-э. д. с. при номинальном режиме
![]()
Так как скорость вращения электродвигателя при этом составляет ![]() , то коэффициент э. д. с.
, то коэффициент э. д. с.
![]()
При неизменном магнитном потоке ![]() — постоянная величина.
— постоянная величина.
Далее, зная значения ![]() , определим э. д. с.
, определим э. д. с. ![]() . Определив э. д. с. Е, найдем скорость вращения:
. Определив э. д. с. Е, найдем скорость вращения: ![]() и, наконец, вращающий момент электродвигателя на валу:
и, наконец, вращающий момент электродвигателя на валу: ![]() , где
, где ![]() — мощность на валу, кВт.
— мощность на валу, кВт.
Составим табл. 12 для определения значений ![]() .
.
Таблица 12
| 2 | 12,5 | 25 | 37,5 | 50 | 62,5 |
| 0,5 | 3,1 | 6,25 | 9,37 | 12,5 | 15,6 |
| 219,5 | 216,9 | 213,75 | 210,63 | 207,5 | 204,4 |
| 1060 | 1048 | 1032 | 1017 | 1000 | 987 |
| 0 | 2271 | 4904 | 7459 | 9935 | 12334 |
| 0 | 20,6 | 41,98 | 69,94 | 94,70 | 119,98 |
| ||||||
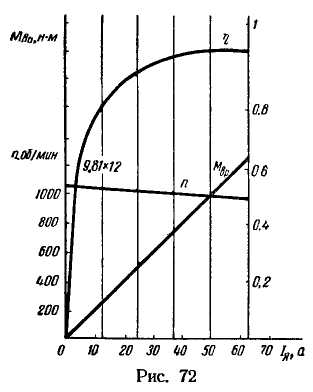
На основании данных табл. 12 построены характеристики ![]() (рис. 72).
(рис. 72).
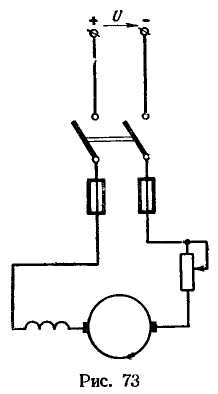
13. Электродвигатель постоянного тока последовательного возбуждения включен в сеть напряжением U = 220 В (рис. 73). Номинальная скорость вращения ![]() . Номинальный вращающий момент
. Номинальный вращающий момент ![]() . Сопротивление обмотки якоря
. Сопротивление обмотки якоря ![]() , сопротивление обмотки возбуждения
, сопротивление обмотки возбуждения ![]() , к. п. д. двигателя
, к. п. д. двигателя ![]() .
.
Определить:
1) номинальную мощность на валу электродвигателя;
2) мощность на входе в электродвигатель;
3) ток электродвигателя;
4) мощность потерь в обмотке якоря и обмотке возбуждения;
5) сопротивление пускового реостата для возможности пуска с кратностью пускового тока ![]() ;
;
6) пусковой момент при пуске согласно п. 5, если известно, что увеличение тока возбуждения в 2,5 раза соответствует увеличению магнитного потока в 1,8 раза.
Решение:
Номинальная мощность на валу двигателя
![]()
Мощность на входе в электродвигатель
![]()
В двигателе последовательного возбуждения ![]() или
или
![]()
Зная ток и сопротивление обмотки якоря, легко определить мощность потерь в обмотке якоря:
![]()
Аналогично определяем мощность потерь в обмотке возбуждения:
![]()
По условию,
![]()
Сопротивление пускового реостата
![]()
где ![]() — пусковой ток якоря.
— пусковой ток якоря.
Для определения величины пускового момента воспользуемся формулой
![]()
Отношение пускового момента к номинальному моменту
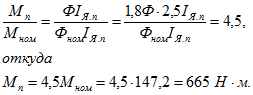
Двигатели последовательного возбуждения обладают весьма большим пусковым моментом. Это свойство особенно ценно в случае применения их в качестве тяговых двигателей.
14. В схеме генератор—двигатель непосредственно к щеткам генератора постоянного тока независимого возбуждения присоединен якорь электродвигателя постоянного тока (рис. 74). В эту цепь входят сопротивления: 1) обмотки якоря генератора ![]() ; 2) обмотки якоря двигателя
; 2) обмотки якоря двигателя ![]() ; 3) щеток генератора
; 3) щеток генератора ![]() ; 4) щеток двигателя
; 4) щеток двигателя ![]() ; 5) проводов (и другие неучтенные сопротивления)
; 5) проводов (и другие неучтенные сопротивления) ![]() ; э. д. с. генератора
; э. д. с. генератора ![]() , противо-э. д. с. двигателя
, противо-э. д. с. двигателя ![]() .
.
Составить баланс мощностей.
Решение:
Ток в контуре, образованном обмотками якоря генератора и двигателя,
![]()
Мощность генератора
![]()
Механическая мощность электродвигателя
![]()
Потери мощности в обмотке якоря генератора
![]()
Потери мощности в обмотке двигателя
![]()
Потери мощности в щетках генератора
![]()
Потери мощности в щетках двигателя
![]()
Потери мощности в проводах
![]()
Очевидно,
![]()
Так как правая часть равенства
![]()
Коэффициент полезного действия в рассмотренном контуре
![]()
При помощи реостата ![]() изменяют ток в обмотке возбуждения генератора и регулируют напряжение на щетках как генератора, так и двигателя, а следовательно, регулируют скорость вращения электродвигателя. При этом в главном контуре, образованном обмотками якоря генератора и двигателя, отсутствует пусковой реостат и не происходит связанных с реостатом потерь энергии.
изменяют ток в обмотке возбуждения генератора и регулируют напряжение на щетках как генератора, так и двигателя, а следовательно, регулируют скорость вращения электродвигателя. При этом в главном контуре, образованном обмотками якоря генератора и двигателя, отсутствует пусковой реостат и не происходит связанных с реостатом потерь энергии.