Расчет цепей с несинусоидальными периодическими ЭДС, напряжениями и токами
Если в линейной цепи действует один или несколько источников несинусоидальных периодических ЭДС и токов, то расчет такой цепи распадается на три этапа:
1. Разложение ЭДС и токов источников на постоянную и синусоидальные составляющие (получение дискретного спектра).
2. Применение принципа наложения и расчет токов и напряжений в цепи для каждой из составляющих в отдельности.
3. Совместное рассмотрение решений, полученных для каждой из составляющих.
Суммирование составляющих в общем виде часто бывает затруднительно и далеко не всегда необходимо, так как уже на основании дискретного спектра можно судить о форме кривой и об основных величинах, ее характеризующих.
Рассмотрим второй этап, представляющий собой основную часть расчета.
Если, например, несинусоидальная ЭДС представлена в виде суммы постоянной и синусоидальных составляющих, то источник несинусоидальной ЭДС можно рассматривать как последовательное соединение источника постоянной ЭДС и источников синусоидальных ЭДС с различными частотами.
Так, если ЭДС (рис. 12.13, а)
![]()
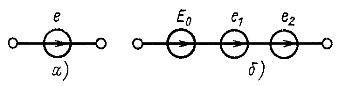
то действие источника такой ЭДС аналогично действию трех последовательно соединенных источников ЭДС (рис. 12.13,6):
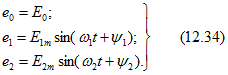
Рис. 12.13
Применив принцип наложения и рассмотрев действие каждой из составляющих ЭДС в отдельности, можно найти составляющие токов во всех участках цепи.
Мгновенное значение тока в цепи равно сумме мгновенных значений составляющих токов. Если, например, в какой-либо ветви токи, создаваемые ЭДС ![]() , соответственно равны
, соответственно равны ![]() , то общий ток
, то общий ток
![]()
Таким образом, расчет линейной цепи с несинусоидальными ЭДС сводится к решению n задач с синусоидальными ЭДС, где n — число синусоидальных составляющих ЭДС различных частот, и одной задачи с постоянными ЭДС.
При решении каждой из этих задач необходимо учитывать, что для различных частот индуктивные и емкостные сопротивления неодинаковы. Индуктивное сопротивление для k-й гармоники в k раз больше, а емкостное, наоборот, в k раз меньше, чем для первой:![]()
Активное сопротивление также зависит от частоты — увеличивается с ростом последней вследствие поверхностного эффекта. Если расчет ведется для гармоник невысоких частот и относительно малых сечений проводов, можно не учитывать изменения сопротивления с частотой и считать, что при всех частотах активное сопротивление равно сопротивлению при постоянном токе.
Если источник несинусоидалыюй ЭДС подключен непосредственно к емкостному элементу, то для k-й гармоники тока![]()
где ![]()
Чем больше k, тем меньше значение емкостного сопротивления для этой гармоники. Следовательно, высшая гармоника ЭДС или напряжения, даже если ее амплитуда составляет незначительную долю амплитуды основной гармоники, может вызвать ток в емкости, соизмеримый с током основной гармоники и даже его превышающий. Поэтому и при напряжении, близком к синусоидальному, ток в емкости может быть резко несинусоидален из-за высших гармоник.
При подключении источника синусоидальной ЭДС к индуктивному элементу ток k-й гармоники![]()
где ![]()
С увеличением порядка k-й гармоники индуктивное сопротивление для этой гармоники возрастает. Поэтому в токе индуктивного элемента высшие гармоники всегда имеют относительно меньшее значение, чем в напряжении; даже при резко несинусоидальной кривой напряжения форма кривой тока нередко приближается к синусоиде.
Если задача поставлена иначе, заданы не ЭДС, а токи несинусоидальных источников, то принцип решения задачи остается тем же.
Источник несинусоидального тока всегда можно представить в виде параллельного соединения ряда источников, синусоидальный ток каждого из которых равен соответствующей составляющей несинусоидального тока. Так, если к узлам ветви или выводам двухполюсника подводится несинусоидальный ток (рис. 12.14, а)![]()
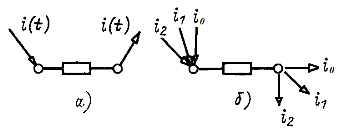
то источник такого тока действует подобно параллельному соединению трех источников (рис. 12.14,6):
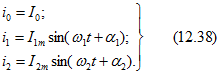
Рис. 12.14
Рассчитав напряжения на сопротивлении от каждой из составляющих тока, легко найти мгновенное значение полного напряжения как сумму отдельных составляющих.
При расчете каждой из гармоник можно пользоваться комплексным методом и строить векторные диаграммы для каждой из гармоник в отдельности. Однако недопустимы суммирование векторов и сложение комплексных напряжении и токов различных гармоник. Действительно, при определении мгновенных значений тока по комплексному необходимо вектор, изображающий комплексную амплитуду каждой гармоники, вращать со своей угловой скоростью ![]() и строить зависимость от времени его проекции на ось мнимых величин.
и строить зависимость от времени его проекции на ось мнимых величин.
Так как для различных гармоник частоты вращения различны, то геометрическое суммирование векторов, изображающих комплексные амплитуды, дает возможность определить мгновенное значение их суммы только в момент времени t = 0 и в общем случае не имеет смысла. При вычерчивании кривых отдельных гармоник следует всегда иметь в виду, что период гармоники обратно пропорционален ее номеру. Следовательно, если по оси абсцисс отложено ![]() , то, соблюдая один и тот же масштаб, вместо углов
, то, соблюдая один и тот же масштаб, вместо углов ![]() надо откладывать углы
надо откладывать углы ![]() .
.
Пример 12.8. В схеме высокочастотного лампового генератора, изображенного на рис. 12.15, а, известны анодный ток i электронной лампы Л, и ЭДС ![]() источника питания. Этот ток при заданных напряжениях на сетке и аноде электронной лампы (в амперах)
источника питания. Этот ток при заданных напряжениях на сетке и аноде электронной лампы (в амперах)
![]()
Найти ток ![]() в источнике питания и гок
в источнике питания и гок ![]() в конденсаторе
в конденсаторе ![]() .
.
Решение. Для определения токов и напряжений необходимо независимо рассчитать три схемы, изображенные на рис. 12.15, б -г. На схемах показаны ЭДС ![]() , токи источников различных частот
, токи источников различных частот ![]() и значения параметров.
и значения параметров.
Рис. 12.15
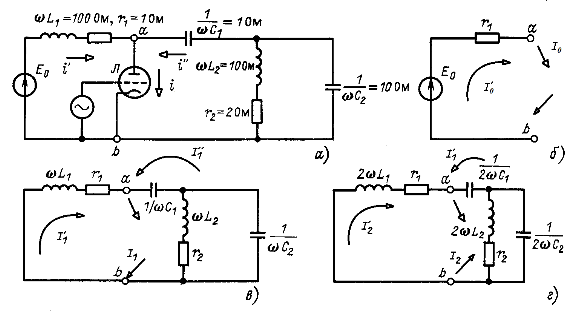
Рис. 12.16
Рассчитав токи в каждой из схем, получаем округленно для постоянной составляющей ![]() , для 1-й гармоники
, для 1-й гармоники ![]() , для 2-й гармоники
, для 2-й гармоники ![]() .
.
Просуммировав мгновенные значения различных гармонических составляющих, получим
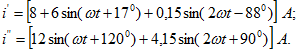
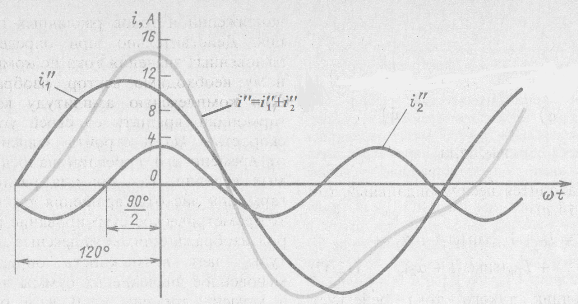
На рис. 12.16 построен график составляющих и результирующего тока ![]() . Так как по оси абсцисс отложено
. Так как по оси абсцисс отложено ![]() , то при построении синусоиды 2-й гармоники начальная фаза (90°) разделена на номер гармоники
, то при построении синусоиды 2-й гармоники начальная фаза (90°) разделена на номер гармоники ![]() .
.
Пример 12.9. Определить напряжения u» на вторичных выводах четырехполюсника в режиме холостого хода при известном напряжении на первичных выводах u‘ (рис. 12.17).
Для четырехполюсника теоретически или экспериментально получена зависимость передаточной функции от частоты![]()
где ![]() — модуль и аргумент комплексной функции
— модуль и аргумент комплексной функции ![]() .
.
Напряжение на первичных выводах представляет собой сигнал, модулированный по амплитуде, спектр которого задан уравнением (12.28).
Решение. Напряжение u‘ на первичных выводах четырехполюсника согласно (12.28)![]()
причем ![]() , и будем искать напряжение на вторичных выводах в виде суммы
, и будем искать напряжение на вторичных выводах в виде суммы![]()
где ![]() .
.
Для рассматриваемого четырехполюсника при холостом ходе
![]()
где ![]() .
.
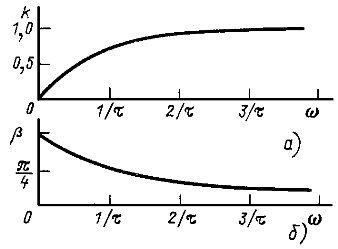
На рис. 12.18, а, б построены графики ![]() .
.
Чтобы рассматриваемый сигнал проходил через четырехполюсник без существенных искажений, т. е. u» мало отличалось от u‘, необходимо выбрать параметры четырехполюсника, удовлетворяющие условию ![]() .
.
Как следует из рис. 12.10 и 12.18, при этом условии напряжения на входе и выходе четырехполюсника практически не будут отличаться, так как для всех трех составляющих сигнала ![]() .
.
Рис. 12.17
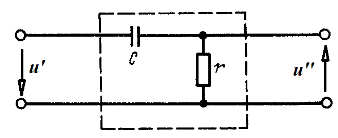
Рис. 12.18
Несинусоидальные токи и напряжения
Периодические несинусоидальные токи и напряжения в электрических цепях
Несинусоидальные ЭДС, напряжения и токи
Разложение периодической несинусоидальной кривой в тригонометрический ряд
Максимальные, действующие и средние значения несинусоидальных периодических ЭДС, напряжений и токов
Коэффициенты, характеризующие форму несинусоидальных периодических кривых
Несинусоидальные кривые с периодической огибающей
Действующие значения ЭДС, напряжений и токов с периодическими огибающими
Расчет цепей с несинусоидальными периодическими ЭДС, напряжениями и токами
Резонанс в цепи несинусоидального тока
Мощность в цепи несинусоидального тока
Высшие гармоники в трехфазных цепях