Включение rL-цепи на синусоидальное напряжение
При включении rL-цепи (см. рис. 14.5) на синусоидальное напряжение ![]() установившийся ток также синусоидальный:
установившийся ток также синусоидальный:![]()
где ![]() , а свободный ток определяется равенством (14.8), так как однородное дифференциальное уравнение прежнее. Переходный ток i равен:
, а свободный ток определяется равенством (14.8), так как однородное дифференциальное уравнение прежнее. Переходный ток i равен:
![]()
В рассматриваемой цепи до включения тока не было. Поэтому при t=0
имеем ![]()
Окончательно получаем
![]()
Напряжение на индуктивности
![]()
При t=0 для напряжения на индуктивности получим ![]() , что легко установить и непосредственно. Действительно, в момент включения напряжение на индуктивном элементе равно напряжению источника, так как напряжение на резистивном
, что легко установить и непосредственно. Действительно, в момент включения напряжение на индуктивном элементе равно напряжению источника, так как напряжение на резистивном ![]() равно нулю.
равно нулю.
Кривая тока i изображена на рис. 14.9, а. Она показывает, что по мере затухания тока ![]() переходный ток стремится к значению установившегося тока. Однако через промежуток времени от T/4 до 3Т/4 после включения, что зависит от угла ψ, ток может достигать значений, превышающих амплитуду установившегося тока.
переходный ток стремится к значению установившегося тока. Однако через промежуток времени от T/4 до 3Т/4 после включения, что зависит от угла ψ, ток может достигать значений, превышающих амплитуду установившегося тока.
Наибольшего возможного значения ток достигает, если в момент включения цепи установившийся ток равен амплитуде, т.е. ![]() (или —π/2), а постоянная времени цепи весьма велика
(или —π/2), а постоянная времени цепи весьма велика ![]() , т. е.
, т. е. ![]() затухает очень медленно.
затухает очень медленно.
Рис. 14.9
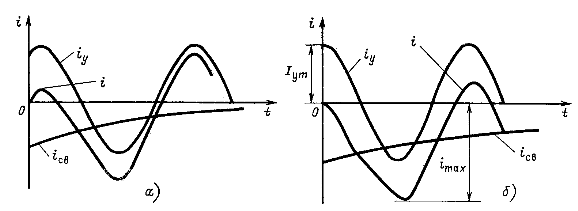
При этих условиях ![]() и приложенное напряжение в момент коммутации проходит через нулевое значение. Кривая тока при
и приложенное напряжение в момент коммутации проходит через нулевое значение. Кривая тока при ![]() и достаточно больших значениях t приведена на рис. 14.9, б. Примерно через половину периода после включения цепи ток достигает почти удвоенной амплитуды установившегося тока
и достаточно больших значениях t приведена на рис. 14.9, б. Примерно через половину периода после включения цепи ток достигает почти удвоенной амплитуды установившегося тока ![]() .
.
Итак, при включении rL-цепи к источнику синусоидального напряжения переходный ток ни при каких условиях не может превысить удвоенной амплитуды установившегося тока.
Начальное значение свободного тока равно абсолютному значению и противоположно по знаку начальному значению установившегося тока. Поэтому, если в момент включения установившийся ток проходит через нуль, то начальное значение свободного тока также равно нулю. Свободный ток вообще не возникает, и в цепи сразу устанавливается установившийся режим. Это будет, как показывает формула (14.16), при ![]() или
или ![]() .
.
В разветвленной цепи с одним индуктивным элементом постоянная времени свободной составляющей любого из токов![]()
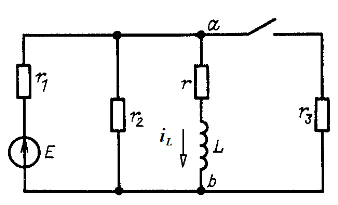
где rвх — входное сопротивление цепи по отношению к выводам ветви с индуктивным элементом, например для цепи рис. 14.10 после коммутации![]()
Рис. 14.10
Переходные процессы
Переходные процессы в электрических цепях
Законы коммутации
Переходный, установившийся и свободный процессы
Короткое замыкание rL-цепи
Включение rL-цепи на постоянное напряжение
Включение rL-цепи на синусоидальное напряжение
Короткое замыкание rС-цепи
Включение rC-цепи на постоянное напряжение
Включение rC-цепи на синусоидальное напряжение
Переходные процессы в rС-цепи
Апериодическая разрядка конденсатора
Предельный случай апериодической разрядки конденсатора
Периодическая (колебательная) разрядка конденсатора
Включение rLC-цепи на постоянное напряжение
Общий случай расчета переходных процессов классическим методом
Пример классического метода
Переходные процессы в цепях с взаимной индуктивностью
Включение пассивного двухполюсника к источнику непрерывно меняющегося напряжения
Включение пассивного двухполюсника к источнику напряжения произвольной формы
Переходная и импульсная переходная характеристики
Запись интеграла Дюамеля при помощи импульсной переходной характеристики
Метод переменных состояния
Численные методы решения уравнений состояния
Дискретные модели электрической цепи
Переходные процессы при некорректных коммутациях
Определение переходного процесса при воздействии периодических импульсов напряжения