Топологические графы
При изложении методов расчета электрических цепей иногда целесообразно применять некоторые топологические понятия, к числу которых относятся, в частности, направленные и ненаправленные топологические графы.
Как следует из первого закона Кирхгофа (1.19), вид уравнений зависит не от элементов ветвей, соединенных в узлах, а от геометрической структуры самих соединений. Аналогичный смысл имеет уравнение (1.20а), выражающее второй закон Кирхгофа. Но, конечно, токи и напряжения зависят не только от геометрической структуры цепи, но и от элементов соответствующих ветвей, что непосредственно следует из закона Ома для участка цепи с ЭДС (1.12а).
Для характеристики геометрической структуры схемы цепи можно пользоваться графом, части которого, называемые ветвями (ребрами), изображают ветви схемы, а точки их соединения, называемые узлами (вершинами), изображают узлы схемы.
На рис. 1.14, б показан ненаправленный (неориентированный) граф для схемы, изображенной на рис. 1.14, а, где каждая из ветвей этого графа (рис. 1.14, б) соответствует определенной ветви схемы (рис. 1.14, а).
Направленным (ориентированным) топологическим графом называется такой, у которого каждая ветвь имеет определенное направление (ориентацию). Для графов схем электрических цепей направление ветви будем выбирать совпадающим с положительным направлением тока в ветви, что и показано на рис. 1.14, в.
Граф заданной схемы можно изобразить по разному, но каждое изображение должно иметь одинаковое со схемой число узлов, а соединяющим их ветвям можно дать различное начертание (рис. 1.14, в — д).
Для направленного графа (рис. 1.14, в) можно записать уравнения на основании первого (1.19) и второго (1.20а) законов Кирхгофа в следующем виде:
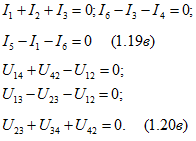
при этом три уравнения (1.19в) совпадают с уравнениями (1.21а), а последние три уравнения можно преобразовать в уравнения (1.23) и (1.24) при помощи закона Ома для участка цепи с ЭДС (1.12 б). Например, из схемы (рис. 1.14. а) следует, что
![]()
после замены напряжений U14, U42 и U12 в уравнениях для контура 1-4-2-1 (рис. 1.14, в) их правыми частями получается выражение, совпадающее с уравнением (1.23).
Чтобы выбрать независимые контуры, введем еще для графа понятия дерева, пути и ветви связи.
Деревом называется совокупность ветвей, соединяющих все узлы, но не образующих ни одного контура. Например, для графа рис. 1.14, в два из возможных деревьев показаны толстыми линиями на рис. 1.14, г и 1.14, д. Непрерывная последовательность ветвей между какими-либо двумя узлами графа при условии, что любой другой узел встречается не более 1 раза, образует путь. Для части графа, составляющей дерево, между каждой парой узлов существует только один путь. Например, путь между узлами дерева 2 и 3 (рис. 1.14, г) состоит из ветвей 3 и 1. Совместно два пути между теми же узлами графа образуют уже контур, т. е. замкнутый путь. Так, добавление второго пути между узлами 2 и 3, состоящего из ветви 6, образует вместе с ветвями первого пути контур из ветвей 3, 1 и 6. Число ветвей дерева равно У — 1, т. е. числу независимых уравнений, составляемых по первому закону Кирхгофа (два узла можно соединить одной ветвью, три узла — двумя ветвями и т. д.). При добавлении еще одной ветви образуется уже контур.
Ветвью связи (связью, хордой) называется любая из ветвей, не входящая в дерево. Все ветви связи дополняют дерево до графа схемы. На рис. 1.14, г и д ветви связи показаны тонкими линиями. Так как общее число ветвей графа равно В, то граф содержит В — (У — 1) ветвей связи, т. е. как раз столько, сколько необходимо составить независимых уравнений по второму закону Кирхгофа. Например, у графов рис. 1.14, г и д число ветвей В = 6, число узлов У = 4, ветвей дерева У — 1 = 3, ветвей связи В — (У — 1) = 3. Если в каждый контур кроме ветвей дерева войдет одна из ветвей связи, не входящая в другие контуры, то для таких В — (У- 1) главных контуров получится независимая система контурных уравнений. Например, для графа рис. 1.14, г можно записать следующие три независимых уравнения по второму закону Кирхгофа: первое для ветвей дерева 3, 2 и ветви связи 4, второе для ветвей дерева 3, 1 и ветви связи 6, третье для ветвей дерева 2, 1 и ветви связи 5.
Как указывалось, вместо уравнений по первому закону Кирхгофа для узлов можно составить уравнения для сечений. Для упрощения выбора независимых сечений целесообразно проводить их так, чтобы каждое сечение разрезало только одну ветвь дерева — было главным сечением. Число главных сечений равно числу ветвей дерева У — 1, т. е. числу независимых уравнений, которые необходимо составить по первому закону Кирхгофа. На рис. 1.14, д показаны штриховой линией три главных сечения S1, S3 и S4. Нормаль к поверхности сечения или ее положительное направление выбирают совпадающим с положительным направлением соответствующей ветви дерева.
Электрические цепи постоянного тока
Пример расчета цепей постоянного тока
Элементы электрических цепей и схем
Схемы замещения источников энергии
Закон Ома для участка цепи с ЭДС
Баланс мощностей для простой неразветвленной цепи
Законы Кирхгофа и их применение
Топологические графы
Законы Кирхгофа в матричной форме
Метод узловых потенциалов
Метод контурных токов
Уравнения цепи в матричной форме
Расширенные узловые уравнения
Преобразования в линейных электрических схемах
Принцип наложения (суперпозиции)
Свойство взаимности
Входные и взаимные проводимости, коэффициенты передачи
Принцип компенсации. Зависимые источники
Общие замечания о двухполюсниках и многополюсниках
Линейные соотношения между напряжениями и токами
Теорема о взаимных приращениях токов и напряжений
Принцип эквивалентного генератора
Передача энергии от активного двухполюсника к пассивному