Включение пассивного двухполюсника к источнику непрерывно меняющегося напряжения (интеграл Дюамеля)
Пусть произвольный пассивный линейный двухполюсник подключается к источнику непрерывно изменяющегося с момента t = 0 напряжения u (рис. 14.32, а). Требуется найти ток i (или напряжение) в любой ветви двухполюсника (рис. 14.32, 6) после замыкания ключа.
Задачу решим в два приема. Сначала искомую величину найдем при включении двухполюсника на единичный скачок напряжения (напряжение постоянное и численно равно единице).
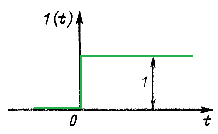
Единичный скачок (единичное ступенчатое воздействие) задается единичной ступенчатой функцией — функцией Хевисайда 1 (t), изображенной на рис. 14.33, которая и представляет собой с точки зрения теории электрических цепей единичное постоянное напряжение (или ток), действующее на входе цепи с момента t = 0+, так что
1 (t) = 0 при t < 0;
1 (t) = 1 при t > 0. (14.77)
Функция h(t), численно равная искомому току (или напряжению), при действии единичного скачка называется переходной функцией или переходной характеристикой. Это реакция цепи на единичный скачок.
Например, для rL-цепи переходная функция тока ![]() (см. раздел), для rС-цепи переходная функция напряжения на емкостном элементе (см. раздел)
(см. раздел), для rС-цепи переходная функция напряжения на емкостном элементе (см. раздел) ![]() . Если определяются и ток, и напряжение, можно соответственно обозначить
. Если определяются и ток, и напряжение, можно соответственно обозначить ![]() .
.
Рис. 14.32
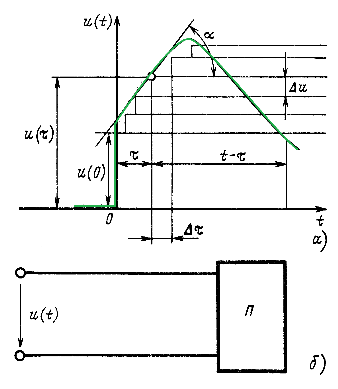
Рис. 14.33
Переходную функцию h(t) при любой схеме пассивного двухполюсника можно найти классическим методом (или операторным методом, или методом интеграла Фурье — см. ниже). Таким образом, в дальнейших расчетах функцию h(t) будем считать известной.
Так как включается пассивный двухполюсник, то при t < 0 токи и напряжения в любой ветви равны нулю. Поэтому при t < 0 следует считать h(t) = 0.
Все дальнейшие рассуждения проведем для случая, когда нужно рассчитать ток.
Непрерывно изменяющееся напряжение u(t) заменим ступенчатой функцией с элементарными прямоугольными скачками Δu (см. рис. 14.32, а). Тогда процесс изменения напряжения можно представить как включение при t=0 постоянного напряжения u(0), а затем как включение элементарных постоянных напряжений Δu, смещенных относительно друг друга на интервалы времени Δτ и имеющих знак плюс для возрастающей и минус для падающей ветви заданной кривой напряжения.
Составляющая искомого тока в момент t от постоянного напряжения u(0) равна u(0)h(t). Составляющая тока в момент t от элементарного скачка напряжения Δu, включаемого в момент времени τ, равна Δuh(t — τ). Здесь аргументом переходной функции служит время (t — τ), поскольку элементарный скачок напряжения Δu начинает действовать на время τ позднее замыкания ключа, или, иначе говоря, поскольку промежуток времени между моментом τ начала действия этого скачка и моментом времени t равен t — τ.
Элементарный скачок напряжения
![]()
где m — масштабный коэффициент.
Поэтому искомая составляющая тока
![]()
Элементарные скачки напряжения включаются на интервале времени от t = 0 до момента t, для которого определяется искомый ток. Поэтому, суммируя составляющие тока от всех скачков, переходя к пределу при ![]() и учитывая составляющую тока от начального скачка напряжения u(0), получаем
и учитывая составляющую тока от начального скачка напряжения u(0), получаем
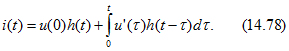
Последняя формула для определения тока при непрерывном изменении приложенного напряжения называется формулой или интегралом Дюамеля (первой формой записи интеграла Дюамеля). Аналогично решается задача при подключении цепи к источнику тока.
Учитывая теорему свертки двух функций ![]()
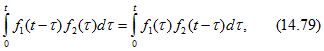
преобразованием (14.78) можно получить и другие формы записи.
Переходные процессы
Переходные процессы в электрических цепях
Законы коммутации
Переходный, установившийся и свободный процессы
Короткое замыкание rL-цепи
Включение rL-цепи на постоянное напряжение
Включение rL-цепи на синусоидальное напряжение
Короткое замыкание rС-цепи
Включение rC-цепи на постоянное напряжение
Включение rC-цепи на синусоидальное напряжение
Переходные процессы в rС-цепи
Апериодическая разрядка конденсатора
Предельный случай апериодической разрядки конденсатора
Периодическая (колебательная) разрядка конденсатора
Включение rLC-цепи на постоянное напряжение
Общий случай расчета переходных процессов классическим методом
Пример классического метода
Переходные процессы в цепях с взаимной индуктивностью
Включение пассивного двухполюсника к источнику непрерывно меняющегося напряжения
Включение пассивного двухполюсника к источнику напряжения произвольной формы
Переходная и импульсная переходная характеристики
Запись интеграла Дюамеля при помощи импульсной переходной характеристики
Метод переменных состояния
Численные методы решения уравнений состояния
Дискретные модели электрической цепи
Переходные процессы при некорректных коммутациях
Определение переходного процесса при воздействии периодических импульсов напряжения