Максимальные, действующие и средние значения несинусоидальных периодических ЭДС, напряжений и токов
Периодически изменяющаяся несинусоидальная величина ![]() помимо своих гармонических составляющих характеризуется тремя значениями:
помимо своих гармонических составляющих характеризуется тремя значениями:
максимальным значением за период ![]() , средним квадратичным за период или действующим значением
, средним квадратичным за период или действующим значением
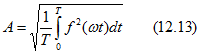
и средним по модулю значением
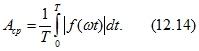
Если кривая ![]() симметрична относительно оси абсцисс и в течение половины периода функция
симметрична относительно оси абсцисс и в течение половины периода функция ![]() ни разу не изменяет знака, то среднее по модулю значение равно среднему значению за половину периода:
ни разу не изменяет знака, то среднее по модулю значение равно среднему значению за половину периода:
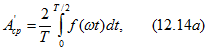
причем в последнем выражении начало отсчета времени должно быть выбрано так, чтобы ![]() . Если за весь период функция ни разу не изменяет знака (см., например, рис. 12.4, б), то среднее по модулю значение равно постоянной составляющей
. Если за весь период функция ни разу не изменяет знака (см., например, рис. 12.4, б), то среднее по модулю значение равно постоянной составляющей ![]() .
.
При несинусоидальных периодических процессах, как и при синусоидальных, обычно под значением ЭДС, тока или напряжения понимают действующее значение.
Если кривая периодически изменяющейся величины разложена в тригонометрический ряд, то действующее значение может быть найдено следующим образом:
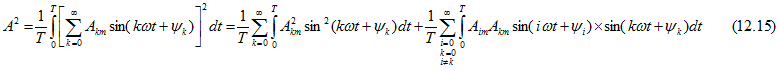
(такое возведение ряда в квадрат вполне допустимо, так как ряд абсолютно сходится при любом значении ![]() ).
).
Каждый из интегралов в последней сумме равен нулю, и, следовательно, равно нулю среднее за период значение от произведений мгновенных значений различных гармонических составляющих функции ![]() . Учитывая это, для действующего значения получим
. Учитывая это, для действующего значения получим
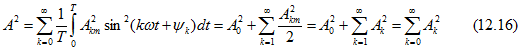
и 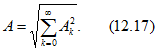
Таким образом, действующее значение периодической несинусоидальной величины зависит только от действующих значений ее гармоник и не зависит от их начальных фаз ![]() .
.
Если, например, напряжение и состоит из ряда гармоник ![]() и т. д., действующие значения которых
и т. д., действующие значения которых ![]() и т. д., то действующее напряжение
и т. д., то действующее напряжение
![]()
Аналогично для тока i
![]()
Часто среднее по модулю и действующее значения несинусоидальной величины могут быть рассчитаны непосредственно на основании интегральных соотношений (12.14) и (12.13). В этих случаях нет необходимости в предварительном разложении функции на гармонические составляющие.
Пример 12.5. Найти средние по модулю и действующие значения функций, изображенных на рис. 12.8.
Решение. Для функции, изображенной на рис. 12.8, а, непосредственно из определения действующего и среднего по модулю значений следует, что ![]() . В случае рис. 12.8, б по (12.13)
. В случае рис. 12.8, б по (12.13)
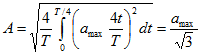
и по (12.14)
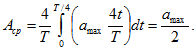
В случае 12.8, в по (12.13)
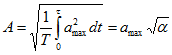
и по (12.14)
![]()
Расчет действующего значения по (12.17) приводит к тем же результатам.
Рис. 12.8
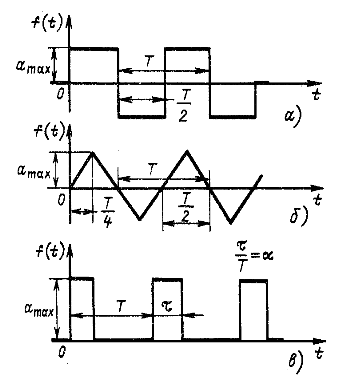
Несинусоидальные токи и напряжения
Периодические несинусоидальные токи и напряжения в электрических цепях
Несинусоидальные ЭДС, напряжения и токи
Разложение периодической несинусоидальной кривой в тригонометрический ряд
Максимальные, действующие и средние значения несинусоидальных периодических ЭДС, напряжений и токов
Коэффициенты, характеризующие форму несинусоидальных периодических кривых
Несинусоидальные кривые с периодической огибающей
Действующие значения ЭДС, напряжений и токов с периодическими огибающими
Расчет цепей с несинусоидальными периодическими ЭДС, напряжениями и токами
Резонанс в цепи несинусоидального тока
Мощность в цепи несинусоидального тока
Высшие гармоники в трехфазных цепях