Определение рабочих точек на характеристиках нелинейных двухполюсников и четырехполюсников
Если для нелинейного двухполюсника нелинейная характеристика задается функцией одного переменного i(u), то характеристика нелинейного четырехполюсника, как указывалось, описывается двумя функциями двух переменных. Одна из этих переменных обычно является аргументом, а вторая — параметром, и функция задается семейством кривых, полученных для различных постоянных значений параметра.
При описании нелинейного четырехполюсника эти две функции и их аргументы и параметры могут быть выбраны различно. Так, для нелинейного четырехполюсника, показанного на рис. 22.8, его характеристики можно задать уравнениями для входа ![]() , для выхода
, для выхода ![]() , для напряжений
, для напряжений ![]() , для токов
, для токов ![]() . Здесь в скобках первая величина является аргументом, а вторая — параметром. Выбор той или иной пары уравнений и аргументов и параметров обусловлен удобством решения поставленных конкретных задач.
. Здесь в скобках первая величина является аргументом, а вторая — параметром. Выбор той или иной пары уравнений и аргументов и параметров обусловлен удобством решения поставленных конкретных задач.
Теория нелинейных четырехполюсников получила наиболее широкое развитие в связи с применением транзисторов. В качестве характеристик такого четырехполюсника обычно применяются зависимости напряжений от токов для входа и выхода, причем в качестве параметра для характеристик входа принимается напряжение на выходе ![]() , а для характеристик выхода — ток на входе
, а для характеристик выхода — ток на входе ![]() .
.
Такие характеристики![]()
называются смешанными. При помощи этих характеристик могут быть легко найдены рабочие точки на нелинейных характеристиках в любых схемах включения четырехполюсников и определены параметры их линейных схем замещения вблизи рабочей точки.
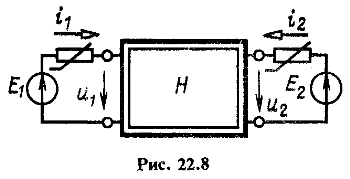
Рассмотрим наиболее общий случай включения нелинейного резистивного четырехполюсника (рис. 22.8), когда его первичная и вторичная цепи подключены к активным нелинейным двухполюсникам с нелинейными характеристиками ![]() . При этом входная и выходная характеристики четырехполюсника заданы семействами характеристик при значениях параметров
. При этом входная и выходная характеристики четырехполюсника заданы семействами характеристик при значениях параметров ![]() для входа и
для входа и ![]() для выхода.
для выхода.
Входную и выходную характеристики построим в третьем и первом квадрантах, как показано на рис. 22.9. Четырехполюсник, к вторичным выводам которого подключен двухполюсник ![]() , можно со стороны первичных выводов рассматривать как некоторый двухполюсник, характеристику которого
, можно со стороны первичных выводов рассматривать как некоторый двухполюсник, характеристику которого ![]() получим простым построением.
получим простым построением.
Для этой цели, начертив в первом квадранте внешнюю характеристику I активного двухполюсника ![]() , прелставляющую собой нагрузочную характеристику на вторичных выводах четырехполюсника, найдем точки пересечения 1, 2, 3 этой характеристики с соответствующими выходными характеристиками четырехполюсника при
, прелставляющую собой нагрузочную характеристику на вторичных выводах четырехполюсника, найдем точки пересечения 1, 2, 3 этой характеристики с соответствующими выходными характеристиками четырехполюсника при ![]() . По этим точкам на оси
. По этим точкам на оси ![]() находим токи
находим токи ![]() . По найденным токам во втором квадранте построим вспомогательную характеристику
. По найденным токам во втором квадранте построим вспомогательную характеристику ![]() (кривая II).
(кривая II).
По значениям параметра ![]() на характеристиках I к II найдем соответствующие значения
на характеристиках I к II найдем соответствующие значения ![]() и для них на входных характеристиках
и для них на входных характеристиках ![]() — точки а, b и с. Соединив эти точки, получим входную характеристику III четырехполюсника, к вторичным выводам которого подключен двухполюсник
— точки а, b и с. Соединив эти точки, получим входную характеристику III четырехполюсника, к вторичным выводам которого подключен двухполюсник ![]() .
.
Таким образом, четырехполюсник с подсоединенным к вторичным выводам двухполюсником эквивалентен двухполюснику с характеристикой III. Рабочую точку А определим как точку пересечения внешней характеристики ![]() (кривая IV) двухполюсника, подсоединенного к первичным выводам четырехполюсника, с входной характеристикой III.
(кривая IV) двухполюсника, подсоединенного к первичным выводам четырехполюсника, с входной характеристикой III.
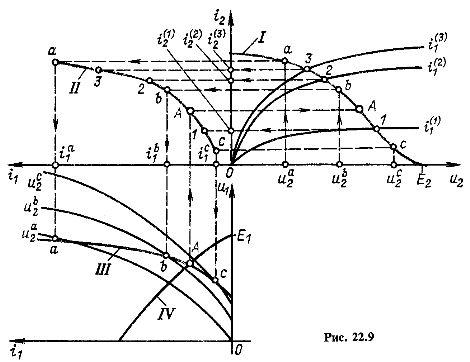
Зная рабочую точку, можно определить дифференциальные параметры линеаризованного четырехполюсника в этой точке, составить эквивалентную схему замещения для переменной составляющей и решать линейную задачу для малых отклонений от рабочей точки. При этом на характеристиках рис. 22.9 процесс изображается некоторой замкнутой кривой или участком прямой, расположенной вблизи точки А, подобно тому как это показано на рис. 22.2.
Изменяя параметры двухполюсников, подключенных к нелинейному четырехполюснику, можно изменять положение рабочей точки А на характеристике четырехполюсника и таким образом управлять параметрами эквивалентной линейной цепи, преобразующей переменный сигнал, как, например, в различного рода электронных усилителях переменного тока.
При построении цепи с нелинейными четырехполюсниками обычно исходят из желаемой рабочей точки на характеристике и соответствующим выбором сопротивлений резисторов и постоянных ЭДС источников питания обеспечивают требуемый режим.
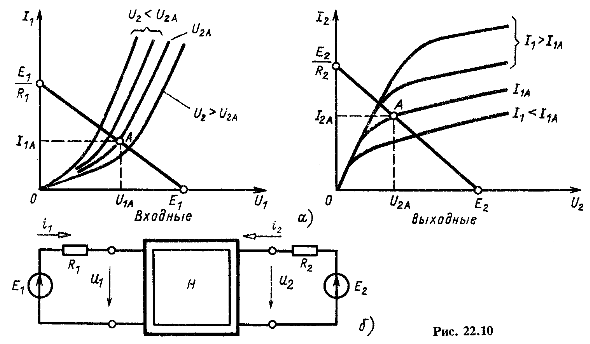
Пусть, например, для нелинейного четырехполюсника известны семейства входных характеристик ![]() при заданных
при заданных ![]() и выходных
и выходных ![]() при заданных
при заданных ![]() (рис. 22.10, а). Если к выводам четырехполюсника подключены источники (рис. 22.10, б) с ЭДС
(рис. 22.10, а). Если к выводам четырехполюсника подключены источники (рис. 22.10, б) с ЭДС ![]() и сопротивлениями
и сопротивлениями ![]() , то для входной и выходной цепей уравнения Кирхгофа имеют вид
, то для входной и выходной цепей уравнения Кирхгофа имеют вид
![]()
На рис. 22.10, а эти уравнения выражаются прямыми, проходящими через рабочую точку А на входной и выходной характеристиках. При анализе цепи, задаваясь ЭДС ![]() и сопротивлениями
и сопротивлениями ![]() , по точкам пересечения прямых с характеристиками определяют рабочую точку А. При синтезе, наоборот, выбрав рабочую точку А на входной и выходной характеристиках и подставив значения
, по точкам пересечения прямых с характеристиками определяют рабочую точку А. При синтезе, наоборот, выбрав рабочую точку А на входной и выходной характеристиках и подставив значения ![]() для рабочей точки А, по формулам (22.10) определяют необходимые значения
для рабочей точки А, по формулам (22.10) определяют необходимые значения ![]() (считая, что ЭДС
(считая, что ЭДС ![]() известны).
известны).
Пусть, например, для нелинейного четырехполюсника известны семейства входных характеристик ![]() при заданных
при заданных ![]() и выходных
и выходных ![]() при заданных
при заданных ![]() (рис. 22.10, а). Если к выводам четырехполюсника подключены источники (рис. 22.10, б) с ЭДС
(рис. 22.10, а). Если к выводам четырехполюсника подключены источники (рис. 22.10, б) с ЭДС ![]() и сопротивлениями
и сопротивлениями ![]() , то для входной и выходной цепей уравнения Кирхгофа имеют вид
, то для входной и выходной цепей уравнения Кирхгофа имеют вид
![]()
На рис. 22.10, а эти уравнения выражаются прямыми, проходящими через рабочую точку А на входной и выходной характеристиках. При анализе цепи, задаваясь ЭДС ![]() и сопротивлениями
и сопротивлениями ![]() , по точкам пересечения прямых с характеристиками определяют рабочую точку А. При синтезе, наоборот, выбрав рабочую точку А на входной и выходной характеристиках и подставив значения
, по точкам пересечения прямых с характеристиками определяют рабочую точку А. При синтезе, наоборот, выбрав рабочую точку А на входной и выходной характеристиках и подставив значения ![]() для рабочей точки А, по формулам (22.10) определяют необходимые значения
для рабочей точки А, по формулам (22.10) определяют необходимые значения ![]() (считая, что ЭДС
(считая, что ЭДС ![]() известны).
известны).
Общая характеристика нелинейных цепей и методов их расчета
Нелинейные электрические и магнитные цепи
Нелинейные двухполюсники и четырехполюсники
Определение рабочих точек на характеристиках нелинейных двухполюсников и четырехполюсников
Схема замещения нелинейного четырехполюсника для переменной составляющей тока и ее параметры
Явления в нелинейных иепях постоянного и переменного токов
Методы расчета нелинейных цепей
О применимости методов расчета и принципов линейной электротехники к нелинейным цепям
Аналитическое описание нелинейных характеристик