Переходные характеристики. Расчет переходных процессов с помощью интеграла Дюамеля
1. Рассчитать переходную проводимость y(t) цепи (рис. 8.38) и переходную функцию h(t) по напряжению. Дано:![]() .
.
Решение:
1. Определим ток ![]() в цепи схемы при подключении к ее зажимам 1 — 1′ в начальный момент t=0 постоянного воздействия в виде напряжения
в цепи схемы при подключении к ее зажимам 1 — 1′ в начальный момент t=0 постоянного воздействия в виде напряжения ![]() :
:
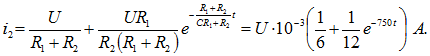
Разделив это выражение на амплитуду воздействия U, найдем значение переходной проводимости:
![]()
2. Выходное напряжение, по закону Ома:
![]()
Разделив это выражение на U, получим переходную функцию передачи по напряжению:
![]()
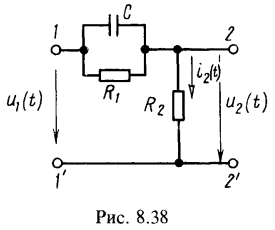
2. Цепь, состоящая из последовательно соединенных R и С, включается на прямоугольный импульс напряжения U, действующий в течение времени ![]() (рис. 8.44, а). Найти выражение напряжения на емкости
(рис. 8.44, а). Найти выражение напряжения на емкости ![]() и ток
и ток ![]() в зависимости от времени. Построить кривые
в зависимости от времени. Построить кривые ![]() .
.
Решение:
Расчет ![]() ведем с помощью интеграла Дюамеля. В рассматриваемом случае функция подводимого напряжения
ведем с помощью интеграла Дюамеля. В рассматриваемом случае функция подводимого напряжения ![]() в момент
в момент ![]() претерпевает скачок, поэтому для решения должны быть использованы формулы. Сначала найдем входящие в эти формулы величины:
претерпевает скачок, поэтому для решения должны быть использованы формулы. Сначала найдем входящие в эти формулы величины:
переходную функцию по напряжению
![]()
напряжение в начальный момент ![]() , производную от заданной функции по новой переменной
, производную от заданной функции по новой переменной ![]() .
.
В интервале времени ![]() (не включая скачок напряжения) по формуле определим
(не включая скачок напряжения) по формуле определим
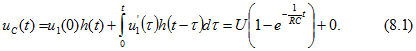
Ток в этом интервале находим с помощью соотношения
![]()
В интервале времени ![]()
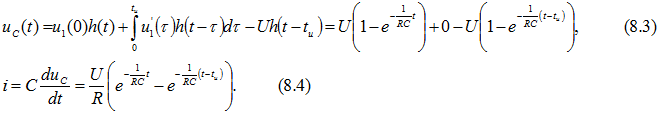
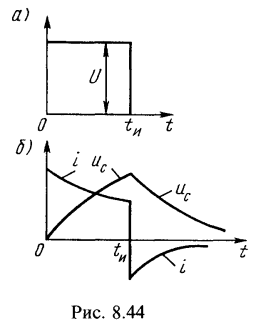
По уравнениям (8.1) — (8.4) на рис. 8.44, б качественно построены кривые ![]() .
.
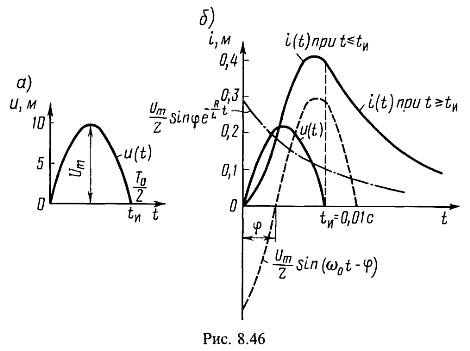
3. Импульс в форме полуволны синусоиды (рис. 8.46, а) включается на цепь, содержащую последовательно соединенные R=10 Ом и L=0,1 Гн.
Напряжение в интервале времени от 0 до ![]() имеет вид
имеет вид ![]() .
.
Найти ток в функции времени.
Решение:
Задачу решим с помощью интеграла Дюамеля. В интервале времени ![]() имеем
имеем
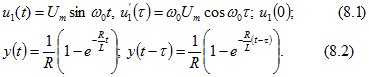
Ток в этом интервале находим по формуле интеграла Дюамеля:
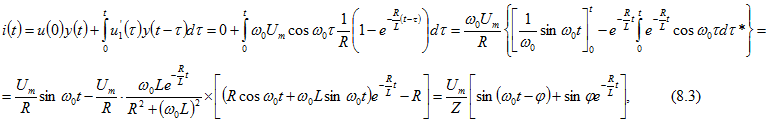
где ![]()
Ток в интервале времени ![]() определяем с помощью интеграла Дюамеля, разбивая интервал интегрирования на два участка: первый участок
определяем с помощью интеграла Дюамеля, разбивая интервал интегрирования на два участка: первый участок ![]() , где выполняются условия (8.1), и второй участок
, где выполняются условия (8.1), и второй участок ![]() , на котором
, на котором ![]() :
: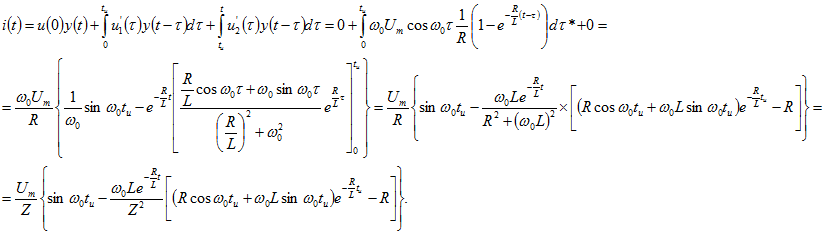
Имея в виду, что ![]() и поэтому
и поэтому ![]() последнее выражение после некоторых упрощений можно привести к виду
последнее выражение после некоторых упрощений можно привести к виду
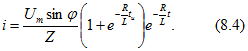
Из выражения (8.3), полученного для первого интервала времени в момент ![]() , ток
, ток
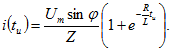
То же значение имеет ток, полученный из выражения (8.4.). Это проверка правильности полученного решения.
По уравнениям (8.3) и (8.4) на рис. 8.58, б построена (в масштабе) кривая тока.
* Этот интеграл является табличным и определяется по формуле
![]()